Integrability and Chaos via fractal analysis of Spectral Form Factors - Gaussian approximations and exact results
Abstract
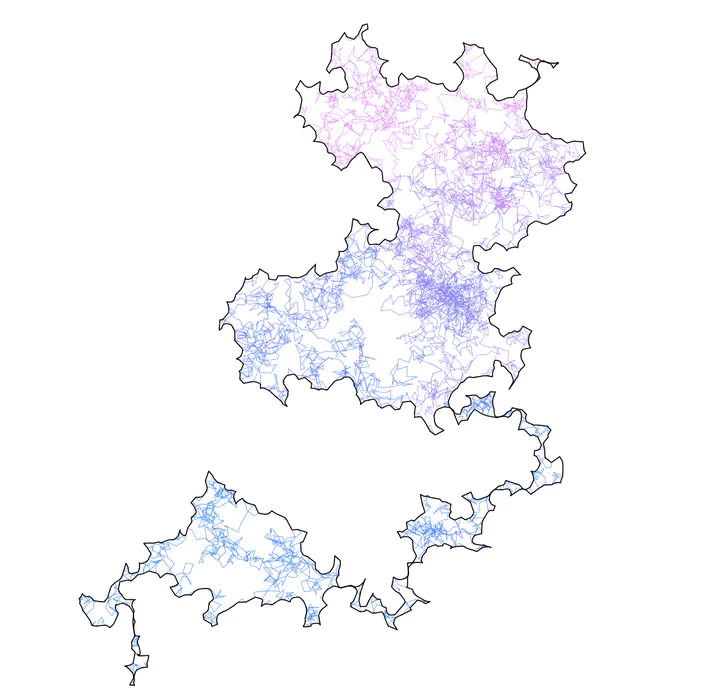
We establish the mathematical equivalence between the spectral form factor, a quantity used to identify the onset of quantum chaos and scrambling in quantum many-body systems, and the classical problem of statistical characterization of planar random walks. We thus associate to any quantum Hamiltonian a random process on the plane. We set down rigorously the conditions under which such random process becomes a Wiener process in the thermodynamic limit and the associated distribution of the distance from the origin becomes Gaussian. This leads to the well known Gaussian behavior of the spectral form factor for quantum chaotic (non-integrable) models, which we show to be violated at low temperature. For systems with quasi-free spectrum (integrable), instead, the distribution of the SFF is Log-Normal. We compute all the moments of the spectral form factor exactly without resorting to the Gaussian approximation. Assuming degeneracies in the quantum chaotic spectrum we solve the classical problem of random walker taking steps of unequal lengths. Furthermore, we demonstrate that the Hausdorff dimension of the frontier of the random walk, defined as the boundary of the unbounded component of the complement, approaches 1 for the integrable Brownian motion, while the non-integrable walk approaches that obtained by the Schramm-Loewner Evolution (SLE) with the fractal dimension 4/3. Additionally, we numerically show that Bethe Ansatz walkers fall into a category similar to the non-integrable walkers.